In this page, you will find entries regarding my past and current work, projects and research.
The documents serve as guide to the research projects, and depending on their respective statuses, these documents might be updated regularly.
If you are looking for tutoring services, please refer to the course list the Teaching section.
Traveling Waves of the Hasegawa-Mima Equation
Status: Work in Progess
As part of my Master’s thesis, I am currently investigating the behavior of traveling wave solutions to the Hasegawa-Mima equation, which is given by
\[\frac{\partial }{\partial t}(I-\Delta)u=\{u,\Delta u\} + k\frac{\partial u}{\partial y},\]where \(\{\cdot,\cdot\}\) is the Poisson bracket and the domain is the square with periodic boundary values, ie the torus.
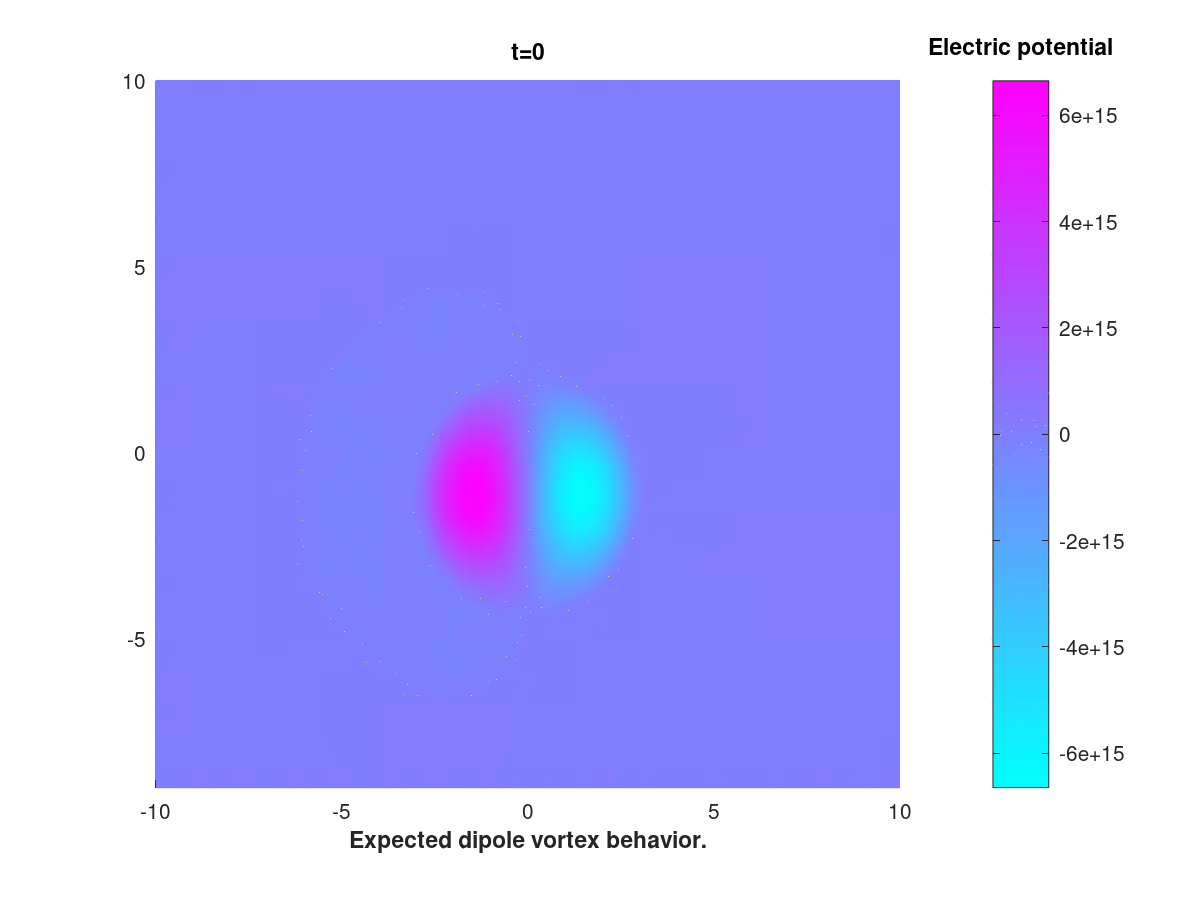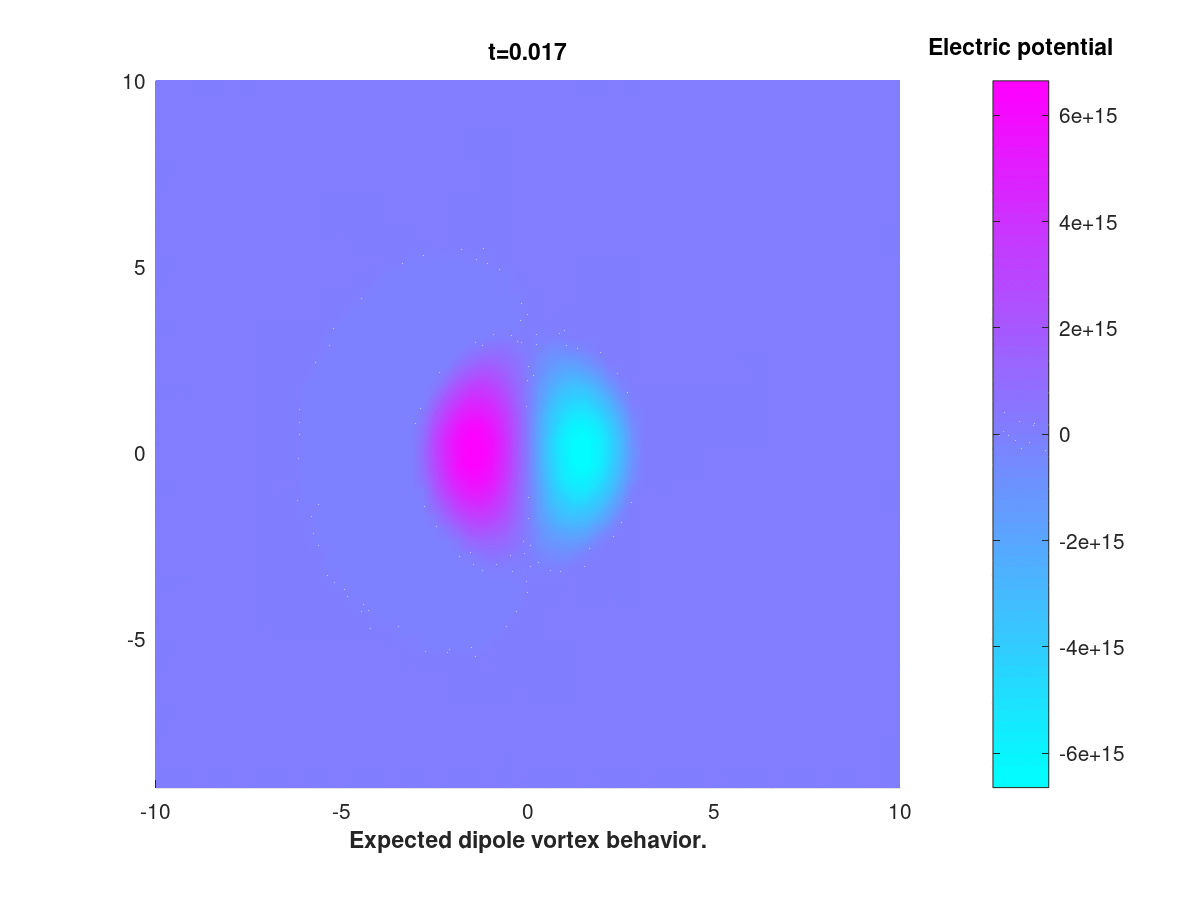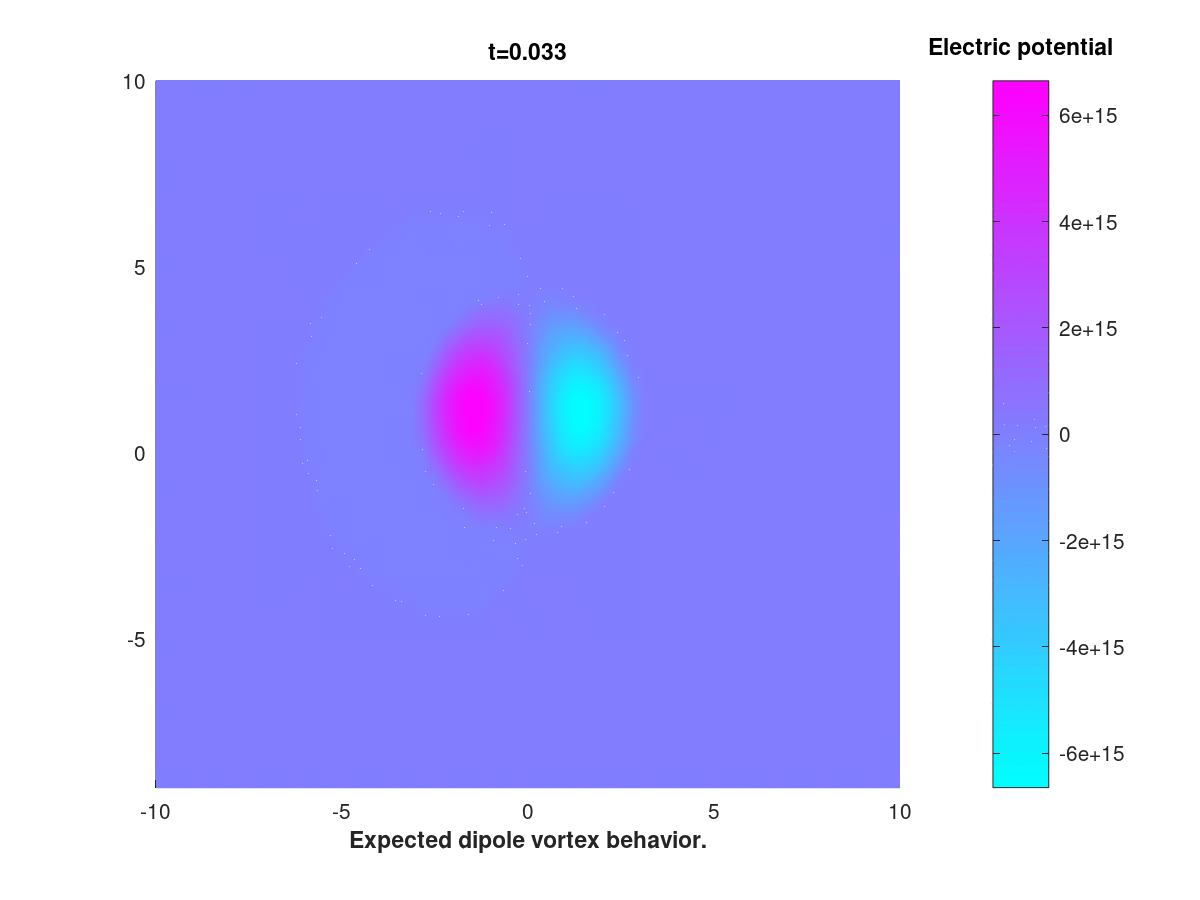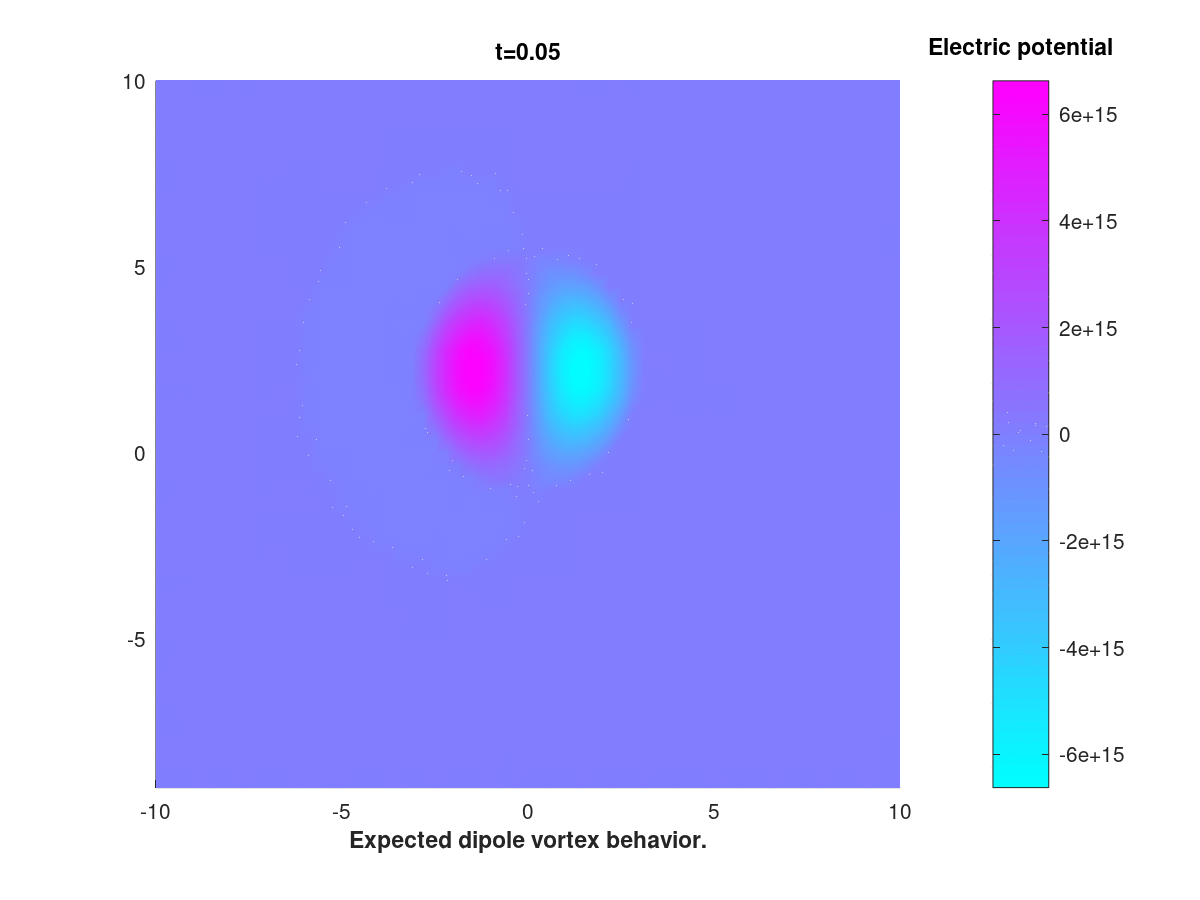
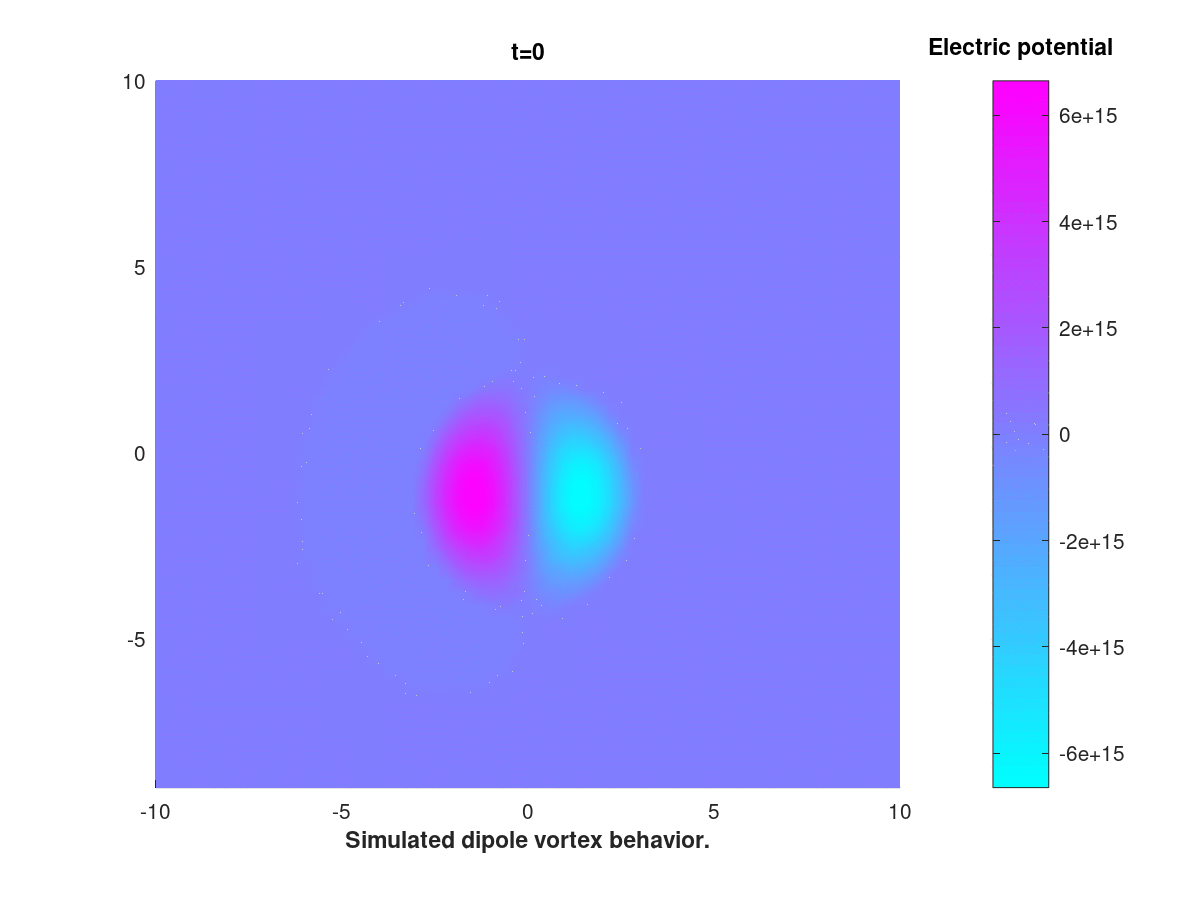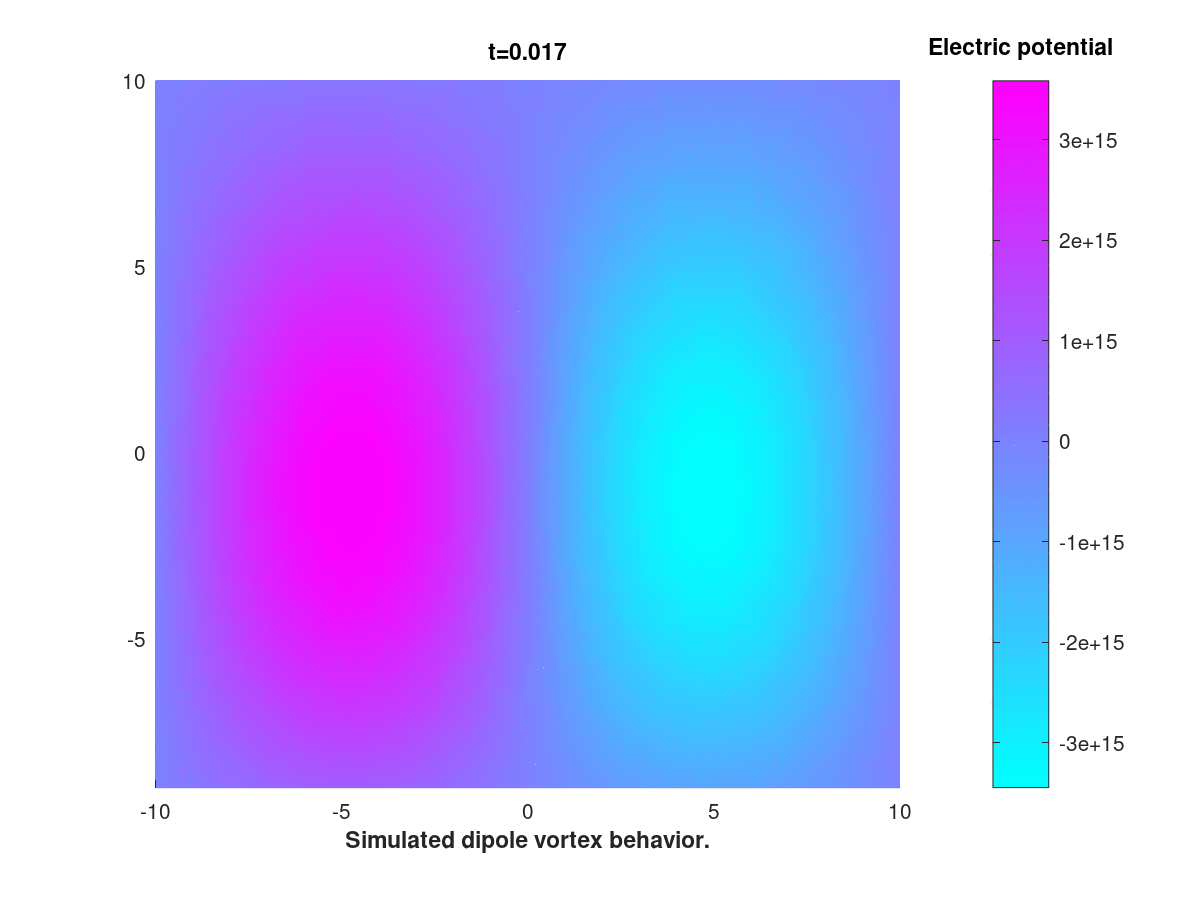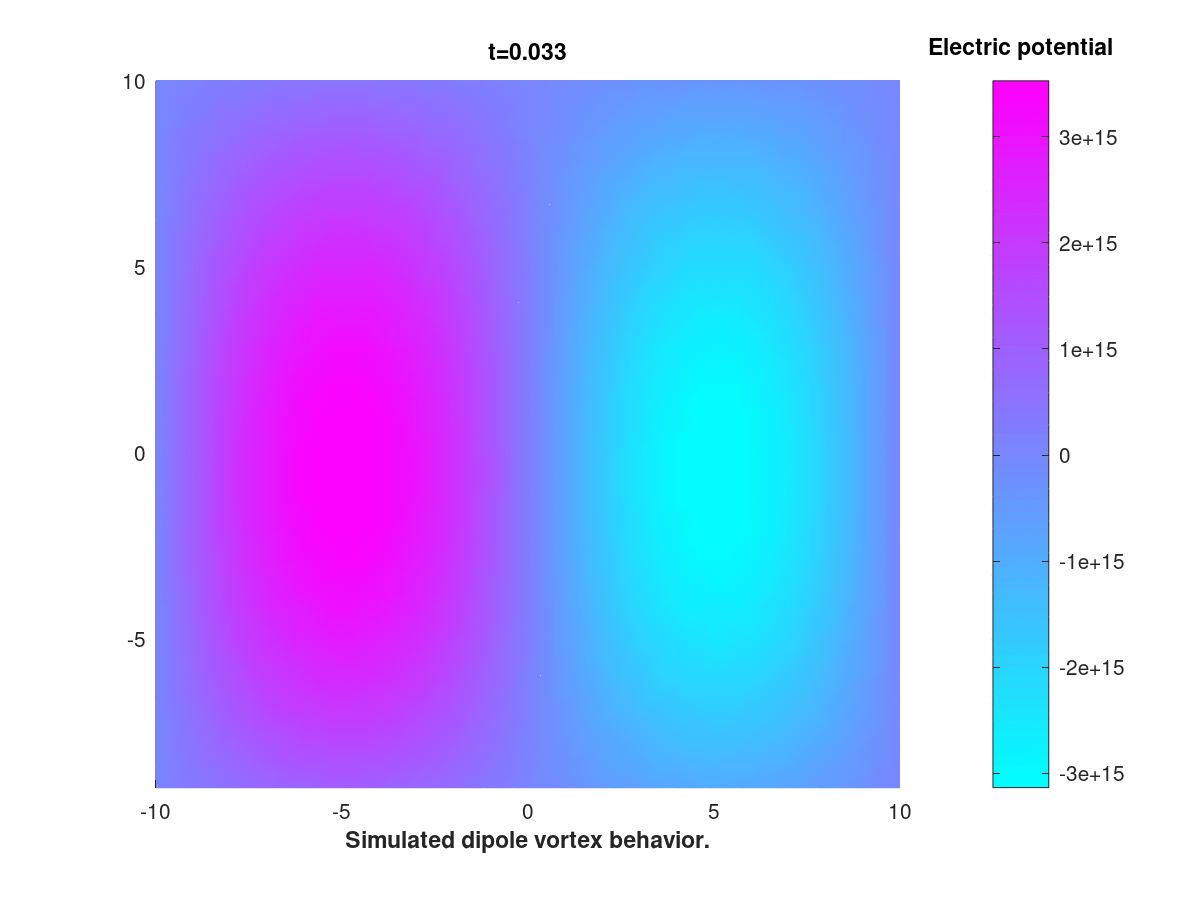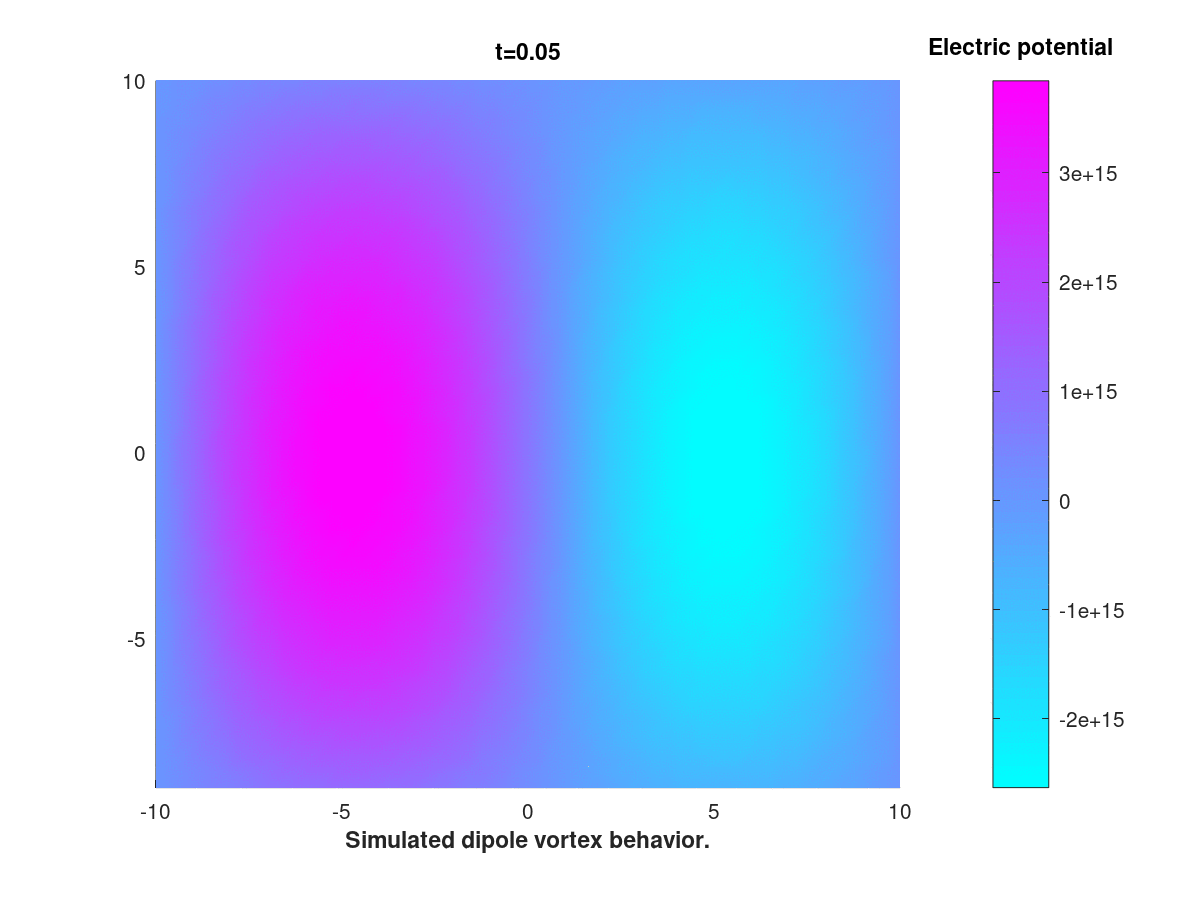
This equation, derived by Hasegawa and Mima in 1978 and bearing resemblence with the Navier-Stokes equation, is used to model turbulent plasma inside a tokamak reactor.
The goal of this inquiry is to adress, numerically and analytically, a certain discrepency between classical results obtained in the literature on one hand, and some more recent results on the other. The numerical method is based of FEM and an IMEX scheme.
- Code: Github repository
Stochastic Analysis
Status: Work in Progess
A project I initiated in early 2021 as part of my self-study of Stochastic Processes. As Stochastic Analysis is my main research interest, I thought it would essential to have a comprehensive reference covering the foundations, all the way from Measure theory to special topics in Stochastic Partial Differential Equations.
The document also focuses on filling out details of the proofs given by authors in the field, with it’s main aim being self-containment and completeness.
Personal Notes on Polynomial Method
Status: Under Revision
These are my personal notes for the Polynomial Method course (MATH 307: Special Topics in Analysis) given by Dr. Bassam Shayya (American University of Beirut).
These notes serve as an introduction to the recent method (2010-2015) used by Larry Guth (MIT) to solve the Erdős distinct distances problem.
A Simulator for Quantum Algorithms
Status: Complete
An ambitious project aimed at simulating MG-QTMs, a generalization of Stationary Rotational Quantum Turing Machines (SR-QTMs). It started out as a final year project for George Zakhour and Bayan Rafeh and is kept under occasional maintenance. I am responsible for developing and maintaining the Arithmetic Logic Unit (ALU) of the Quantum Virtual Machine (QVM for short), which simulates these QTM’s.
.png)
